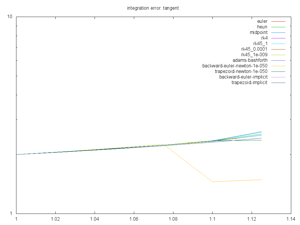
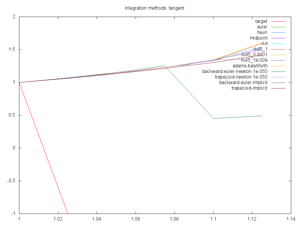
Integration tests.
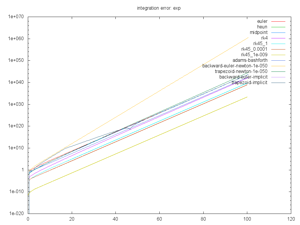
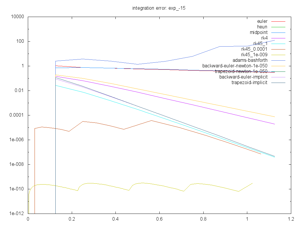
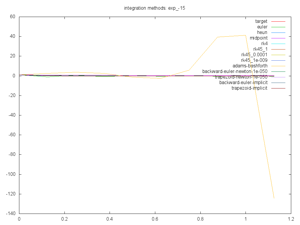
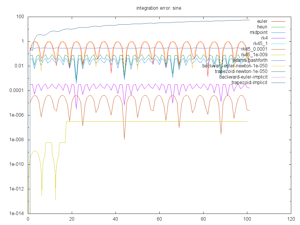
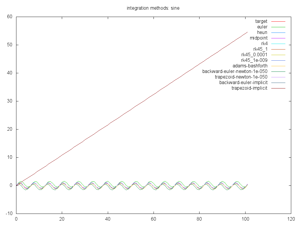
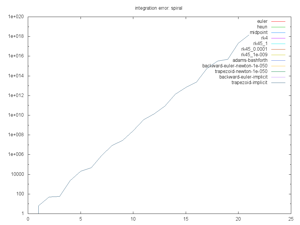
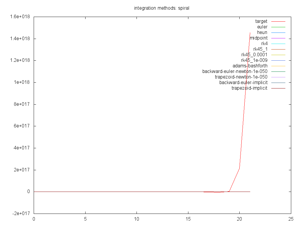
Euler, Heun, Midpoint, and RK4 are all straightforward explicit solvers.
RK45 is adaptive explicit solver.
Adams Bashforth is an iterative solver. It's broken at the moment. Someone give me a hint.
Backwards Euler and Trapezoid Implicit are implicit solvers for which the math was solved per-problem. (Oh yes, I have a Computer Algebra System in the works too). Backwards Euler and Trapezoid Newton are based on a Newton root-finding if no explicit calculations are provided. This rootfinding assumes the change in next function wrt the next x is zero. It produces a simple fixed-point convergence for derivative.
Would like to add quadrature integrators (Gaussian, Hermite, etc) and maybe, to get eccentric, add different fixed-point solvers: root finding based on several-derivative constraints rather than just linear, as Newton uses.