... IDK ... BFF ... Jill.
For an acronym translation, this reads, "Optical Character Recognition via Back-Propagation Neural Networks on the Graphics Processing Unit."
I was toying with the Hopfield neural network that I had wrote, trying it's potential for OCR, and things weren't going too smoothly. Speaking of which, I might have butchered the old demo that showed the memory converging via continuous model on one of several pictures. Now it is a discrete model, the math is tailored a bit closer to the Wolfram page on Hopfield networks, and it attempts to train itself to font characters.
This lead me to sit down and try to work out how exactly Hopfield figured out that this thing would converge, let alone converging accurately for up to 15*m patterns (where m is the number of neurons in the system). I didn't bother with the discrete case at all (though I believe that was Hopfield's original motivation - to simulate biology with circuitry (?)) but skipped right ahead to the continuous. Linearize the system and analyze its convergence. All I can tell from what I'm looking at is that it has several eigenvectors to the system, one of which being the memory pattern. The nonlinear activation function should keep normalizing it to keep the vector from escaping on and on forever, (I 'approximated' it to work like normalization) which means the state vector should be pulled towards the greatest eigenvalued eigenvector. The memory vector. A single vector.
I didn't dig any further. The math fit what I was seeing. I didn't even consult Hopfield's paper. I'll save that for another time.
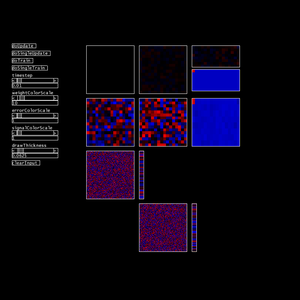
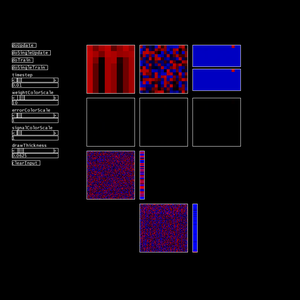
This motivated me to try my hand at a GPU implementation of a feed-forward network and apply it to the task of character recognition.
Initial versions were sketchy. One thing that helped significantly was remapping the bounding box surrounding the used pixels into the input neuron space. I'm tempted to eventually try rotating this several times over to rule out angles, but meh, it seems to work well enough for the time being.